拉格朗日插值

题目大意

给出个点，将过这个点的最多次的多项式记为，求的值。

方法 1：差分法

差分法适用于的情况。

如，用差分法求的多项式形式。

1   5   14   30   55   91
  4   9    16   25   36
    5   7     9   11
      2    2    2

第一行为的连续的前几项；若上面一行有个值，下面一行有个值，每个值为上面对应的相邻两项的差。观察到，如果这样操作的次数足够多（前提是为多项式），每次总会返回一个定值，可以利用这个定值求出的每一项的系数，然后即可将代入多项式中求解。如上例中可求出。时间复杂度为，对给出的点的限制性较强。

方法 2：高斯消元

使用 待定系数法 。设将每个代入，有，这样就可以得到一个由条元次方程所组成的方程组，然后使用 高斯消元 求出每一项，然后将代入求值。

如果您不知道什么是高斯消元，请看 Luogu P3389 高斯消元法。

时间复杂度，对给出点的坐标无要求。

方法 3：拉格朗日插值法

考虑将每个点做一个对于轴的垂线，设垂足为。

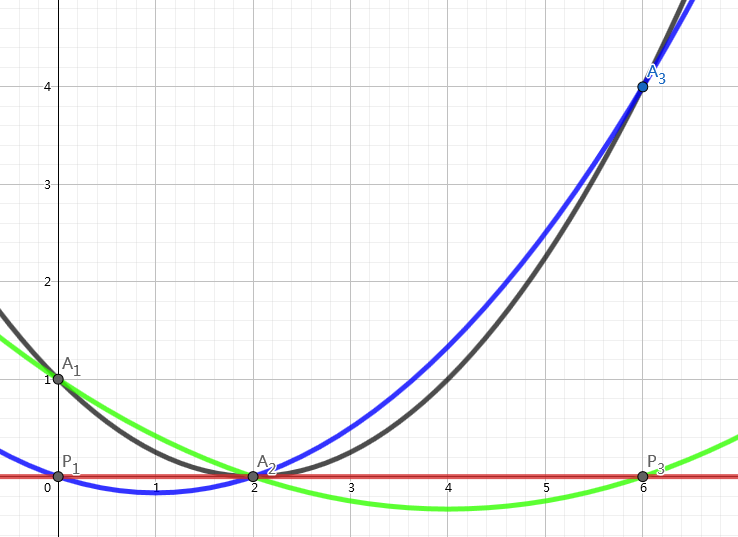
sample

如上图所示，黑线等于蓝线加绿线加红线。每次我们选择个，并选择其他的，做一条过这些点的一条至多次的线。由于有个点都在轴上，我们知道这条线的解析式一定是形如的形式。

最后将所有的相加，即。因为对于每个点，都只有一条函数经过，其余都经过，这一项的系数是，所以最后的和函数总是过所有个点的。

公式整理得：

如果要将每一项都算出来，时间复杂度仍是的，但是本题中只用求出的值，所以只需将代入进式子里得：

本题中，还需要求解逆元。如果先分别计算出分子和分母，再将分子乘进分母的逆元，累加进最后的答案，时间复杂度的瓶颈就不会在求逆元上，时间复杂度为。

代码实现

#include <algorithm>
#include <cstdio>
#include <cstring>
const int maxn = 2010;
using ll = long long;
ll mod = 998244353;
ll n, k, x[maxn], y[maxn], ans, s1, s2;
ll powmod(ll a, ll x) {
  ll ret = 1ll, nww = a;
  while (x) {
    if (x & 1) ret = ret * nww % mod;
    nww = nww * nww % mod;
    x >>= 1;
  }
  return ret;
}
ll inv(ll x) { return powmod(x, mod - 2); }
int main() {
  scanf("%lld%lld", &n, &k);
  for (int i = 1; i <= n; i++) scanf("%lld%lld", x + i, y + i);
  for (int i = 1; i <= n; i++) {
    s1 = y[i] % mod;
    s2 = 1ll;
    for (int j = 1; j <= n; j++)
      if (i != j)
        s1 = s1 * (k - x[j]) % mod, s2 = s2 * ((x[i] - x[j] % mod) % mod) % mod;
    ans += s1 * inv(s2) % mod;
    ans = (ans + mod) % mod;
  }
  printf("%lld\n", ans);
  return 0;
}

贡献者：@Ir1d @TrisolarisHD @YanWQ-monad

本页面最近更新：2/3/2023, 12:00:00 AM，更新历史

发现错误？想一起完善？在 GitHub 上编辑此页！

本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供，附加条款亦可能应用

OI Wiki

拉格朗日插值

题目大意

方法 1：差分法

方法 2：高斯消元

方法 3：拉格朗日插值法

代码实现

0 条评论
未登录用户

拉格朗日插值

题目大意

方法 1：差分法

方法 2：高斯消元

方法 3：拉格朗日插值法

代码实现

0 条评论未登录用户

0 条评论
未登录用户