快速傅里叶变换

前置知识：

本文将介绍一种算法，它支持在 的时间内计算两个 度的多项式的乘法，比朴素的 算法更高效。由于两个整数的乘法也可以被当作多项式乘法，因此这个算法也可以用来加速大整数的乘法计算。

概述

离散傅里叶变换（Discrete Fourier Transform，缩写为 DFT），是傅里叶变换在时域和频域上都呈离散的形式，将信号的时域采样变换为其 DTFT 的频域采样。

FFT 是一种高效实现 DFT 的算法，称为快速傅立叶变换（Fast Fourier Transform，FFT）。它对傅里叶变换的理论并没有新的发现，但是对于在计算机系统或者说数字系统中应用离散傅立叶变换，可以说是进了一大步。快速数论变换 (NTT) 是快速傅里叶变换（FFT）在数论基础上的实现。

在 1965 年，Cooley 和 Tukey 发表了快速傅里叶变换算法。事实上 FFT 早在这之前就被发现过了，但是在当时现代计算机并未问世，人们没有意识到 FFT 的重要性。一些调查者认为 FFT 是由 Runge 和 König 在 1924 年发现的。但事实上高斯早在 1805 年就发明了这个算法，但一直没有发表。

多项式的表示

系数表示法

系数表示法就是用一个多项式的各个项系数来表达这个多项式，即使用一个系数序列来表示多项式：

点值表示法

点值表示法是把这个多项式看成一个函数，从上面选取 个点，从而利用这 个点来唯一地表示这个函数。

设

那么用点值表示法表示 如下

通俗地说，多项式由系数表示法转为点值表示法的过程，就是 DFT 的过程。相对地，把一个多项式的点值表示法转化为系数表示法的过程，就是 IDFT。而 FFT 就是通过取某些特殊的 的点值来加速 DFT 和 IDFT 的过程。

单位复根

考虑这样一个问题：

DFT 是把多项式从系数表示转到了点值表示，那么我们把点值相乘之后，再还原成系数表示，就解决了我们的问题。上述过程如下：

假设我们 DFT 过程对于两个多项式选取的 序列相同，那么可以得到

如果我们设 ，那么容易得到 的点值表达式：

但是我们要的是系数表达式，接下来问题变成了从点值回到系数。如果我们带入到高斯消元法的方程组中去，会把复杂度变得非常高。光是计算 就是 项，这就已经 了，更别说还要把 个方程进行消元……

因此我们不去计算 。 和 的幂都很好算，但是仅仅有两个也不够，我们至少需要 个。利用我们刚学的长度为 的虚数，这些数不管怎么乘长度都是 。我们需要的是 中的 ，容易想到 和 是符合的。除此以外：

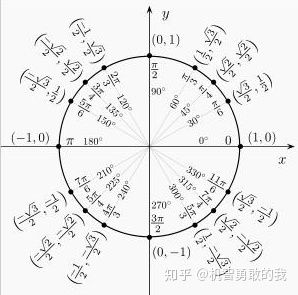
观察上图，容易发现这是一个单位圆（圆心为原点，半径为 ），单位圆上的向量模长均为 ，根据复数的运算法则，两个复数相乘，在复平面上表示为两个向量模长相乘，辐角相加。因此两个模长为 的向量相乘，得到的仍是模长为 的向量，辐角为两个向量辐角的和。因此我们可以将 中的 理解为复平面上的一个单位向量，满足它的辐角的 倍恰好是 ——即把圆周 等分的角。我们把符合以上条件的复数（复平面上的向量）称为复根，用 表示。

定义

严谨地，我们称 在复数意义下的解是 次复根。显然，这样的解有 个，设 ，则 的解集表示为 。我们称 是 次单位复根（the -th root of unity）。根据复平面的知识， 次单位复根是复平面把单位圆 等分的第一个角所对应的向量。其它复根均可以用单位复根的幂表示。

另一方面，根据欧拉公式，还可以得到 。

举个例子，当 时，，即 就是 次单位复根：

当 的时候，相当于把单位圆等分 份。将每一份按照极角编号，那么我们只要知道 （因为它的角度是相当于单位角度），就能知道 。

恒等于 ， 的角度是 的两倍，所以 ，依次以此类推。

性质

单位复根有三个重要的性质。对于任意正整数 和整数 ：

快速傅里叶变换

FFT 算法的基本思想是分治。就 DFT 来说，它分治地来求当 的时候 的值。它的分治思想体现在将多项式分为奇次项和偶次项处理。

举个例子，对于一共 项的多项式

按照次数的奇偶来分成两组，然后右边提出来一个

分别用奇偶次次项数建立新的函数

那么原来的 用新函数表示为

利用单位复根的性质得到

同理可得

因此我们求出了 和 后，就可以同时求出 和 。于是对 和 分别递归 DFT 即可。

考虑到分治 DFT 能处理的多项式长度只能是 ，否则在分治的时候左右不一样长，右边就取不到系数了。所以要在第一次 DFT 之前就把序列向上补成长度为 （高次系数补 ）、最高项次数为 的多项式。

在代入值的时候，因为要代入 个不同值，所以我们代入 一共 个不同值。

代码实现方面，STL 提供了复数的模板，当然也可以手动实现。两者区别在于，使用 STL 的 complex 可以调用 exp 函数求出 。但事实上使用欧拉公式得到的虚数来求 也是等价的。

#include <cmath>
#include <complex>

typedef std::complex<double> Comp;  // STL complex

const Comp I(0, 1);  // i
const int MAX_N = 1 << 20;

Comp tmp[MAX_N];

void DFT(Comp *f, int n, int rev) {  // rev=1,DFT; rev=-1,IDFT
  if (n == 1) return;
  for (int i = 0; i < n; ++i) tmp[i] = f[i];
  for (int i = 0; i < n; ++i) {  // 偶数放左边，奇数放右边
    if (i & 1)
      f[n / 2 + i / 2] = tmp[i];
    else
      f[i / 2] = tmp[i];
  }
  Comp *g = f, *h = f + n / 2;
  DFT(g, n / 2, rev), DFT(h, n / 2, rev);  // 递归 DFT
  Comp cur(1, 0), step(cos(2 * M_PI / n), sin(2 * M_PI * rev / n));
  // Comp step=exp(I*(2*M_PI/n*rev)); // 两个 step 定义是等价的
  for (int k = 0; k < n / 2; ++k) {
    tmp[k] = g[k] + cur * h[k];
    tmp[k + n / 2] = g[k] - cur * h[k];
    cur *= step;
  }
  for (int i = 0; i < n; ++i) f[i] = tmp[i];
}

时间复杂度 。

位逆序置换

这个算法还可以从“分治”的角度继续优化。我们每一次都会把整个多项式的奇数次项和偶数次项系数分开，一直分到只剩下一个系数。但是，这个递归的过程需要更多的内存。因此，我们可以先“模仿递归”把这些系数在原数组中“拆分”，然后再“倍增”地去合并这些算出来的值。

以 项多项式为例，模拟拆分的过程：

• 初始序列为
• 一次二分之后
• 两次二分之后
• 三次二分之后

规律：其实就是原来的那个序列，每个数用二进制表示，然后把二进制翻转对称一下，就是最终那个位置的下标。比如 是 001，翻转是 100，也就是 4，而且最后那个位置确实是 4。我们称这个变换为位逆序置换（bit-reversal permutation，国内也称蝴蝶变换）。

根据它的定义，我们可以在 的时间内求出每个数变换后的结果：

/*
 * 进行 FFT 和 IFFT 前的反置变换
 * 位置 i 和 i 的二进制反转后的位置互换
 *len 必须为 2 的幂
 */
void change(Complex y[], int len) {
  int i, j, k;
  for (int i = 1, j = len / 2; i < len - 1; i++) {
    if (i < j) swap(y[i], y[j]);
    // 交换互为小标反转的元素，i<j 保证交换一次
    // i 做正常的 + 1，j 做反转类型的 + 1，始终保持 i 和 j 是反转的
    k = len / 2;
    while (j >= k) {
      j = j - k;
      k = k / 2;
    }
    if (j < k) j += k;
  }
}

实际上，位逆序变换可以 从小到大递推实现，设 ，其中 表示二进制数的长度，设 表示长度为 的二进制数 翻转后的数（高位补 ）。我们要求的是 。

首先 。

我们从小到大求 。因此在求 时， 的值是已知的。因此我们把 右移一位（除以 ），然后取反，再右移一位，就得到了 除了（二进制）个位 之外其它位的翻转结果。

考虑个位的翻转结果：如果个位是 ，翻转之后最高位就是 。如果个位是 ，则翻转后最高位是 ，因此还要加上 。综上

举个例子：设 ，。为了翻转 ：

1. 考虑 ，我们知道 ，再右移一位就得到了 。
2. 考虑个位，如果是 ，它就要翻转到数的最高位，即翻转数加上 ，如果是 则不用更改。

// 同样需要保证 len 是 2 的幂
// 记 rev[i] 为 i 翻转后的值
void change(Complex y[], int len) {
  for (int i = 0; i < len; ++i) {
    rev[i] = rev[i >> 1] >> 1;
    if (i & 1) {  // 如果最后一位是 1，则翻转成 len/2
      rev[i] |= len >> 1;
    }
  }
  for (int i = 0; i < len; ++i) {
    if (i < rev[i]) {  // 保证每对数只翻转一次
      swap(y[i], y[rev[i]]);
    }
  }
  return;
}

快速傅里叶逆变换

傅里叶逆变换可以用傅里叶变换表示。对此我们有两种理解方式。

线性代数角度

IDFT（傅里叶反变换）的作用，是把目标多项式的点值形式转换成系数形式。而 DFT 本身是个线性变换，可以理解为将目标多项式当作向量，左乘一个矩阵得到变换后的向量，以模拟把单位复根代入多项式的过程：

现在我们已经得到最左边的结果了，中间的 值在目标多项式的点值表示中也是一一对应的，所以，根据矩阵的基础知识，我们只要在式子两边左乘中间那个大矩阵的逆矩阵就行了。由于这个矩阵的元素非常特殊，它的逆矩阵也有特殊的性质，就是每一项取倒数，再除以 ，就能得到它的逆矩阵。

为了使计算的结果为原来的倒数，根据单位复根的性质并结合欧拉公式，可以得到

因此我们可以尝试着把单位根 取成 ，这样我们的计算结果就会变成原来的倒数，而其它的操作过程与 DFT 是完全相同的。我们可以定义一个函数，在里面加一个参数 或者是 ，然后把它乘到 上。传入 就是 DFT，传入 就是 IDFT。

单位复根周期性

利用单位复根的周期性同样可以理解 IDFT 与 DFT 之间的关系。

考虑原本的多项式是 。而 IDFT 就是把你的点值表示还原为系数表示。

考虑 构造法。我们已知 ，求 。构造多项式如下

相当于把 当做多项式 的系数表示法。

这时我们有两种推导方式，这对应了两种实现方法。

方法一

设 ，则多项式 在 处的点值表示法为 。

对 的定义式做一下变换，可以将 表示为

记 。

当 时，。

当 时，我们错位相减

也就是说

那么代回原式

也就是说给定点 ，则 的点值表示法为

综上所述，我们取单位根为其倒数，对 跑一遍 FFT，然后除以 即可得到 的系数表示。

方法二

我们直接将 代入 。

推导的过程与方法一大同小异，最终我们得到 。

当且仅当 时有 ，否则为 。因此 。

这意味着我们将 做 DFT 变换后，反转再除以 ，同样可以还原 的系数表示。

代码实现

所以我们 FFT 函数可以集 DFT 和 IDFT 于一身。代码实现如下：

/*
 * 做 FFT
 * len 必须是 2^k 形式
 * on == 1 时是 DFT，on == -1 时是 IDFT
 */
void fft(Complex y[], int len, int on) {
  change(y, len);
  for (int h = 2; h <= len; h <<= 1) {                  // 模拟合并过程
    Complex wn(cos(2 * PI / h), sin(on * 2 * PI / h));  // 计算当前单位复根
    for (int j = 0; j < len; j += h) {
      Complex w(1, 0);  // 计算当前单位复根
      for (int k = j; k < j + h / 2; k++) {
        Complex u = y[k];
        Complex t = w * y[k + h / 2];
        y[k] = u + t;  // 这就是把两部分分治的结果加起来
        y[k + h / 2] = u - t;
        // 后半个 “step” 中的ω一定和 “前半个” 中的成相反数
        // “红圈”上的点转一整圈“转回来”，转半圈正好转成相反数
        // 一个数相反数的平方与这个数自身的平方相等
        w = w * wn;
      }
    }
  }
  if (on == -1) {
    for (int i = 0; i < len; i++) {
      y[i].x /= len;
    }
  }
}

/*
 * 做 FFT
 * len 必须是 2^k 形式
 * on == 1 时是 DFT，on == -1 时是 IDFT
 */
void fft(Complex y[], int len, int on) {
  change(y, len);
  for (int h = 2; h <= len; h <<= 1) {             // 模拟合并过程
    Complex wn(cos(2 * PI / h), sin(2 * PI / h));  // 计算当前单位复根
    for (int j = 0; j < len; j += h) {
      Complex w(1, 0);  // 计算当前单位复根
      for (int k = j; k < j + h / 2; k++) {
        Complex u = y[k];
        Complex t = w * y[k + h / 2];
        y[k] = u + t;  // 这就是把两部分分治的结果加起来
        y[k + h / 2] = u - t;
        // 后半个 “step” 中的ω一定和 “前半个” 中的成相反数
        // “红圈”上的点转一整圈“转回来”，转半圈正好转成相反数
        // 一个数相反数的平方与这个数自身的平方相等
        w = w * wn;
      }
    }
  }
  if (on == -1) {
    reverse(y, y + len);
    for (int i = 0; i < len; i++) {
      y[i].x /= len;
    }
  }
}